CS231n Lecture 4-1: Backpropagation

빠르고 정확한 Analytic gradient를 유도하고 사용하는 방법에 대해 배워보자.

계산 그래프 (Computational graph)

복잡한 형태의 함수를 나타내기 위해 계산 그래프(computational graph)를 사용할 것이다. 기본적으로 계산 그래프를 통해 어떤 함수든 표현 가능하다. 다음 예시는 $W$, $x$를 입력으로 받는 linear classifier를 계산 그래프로 나타낸 것이다.

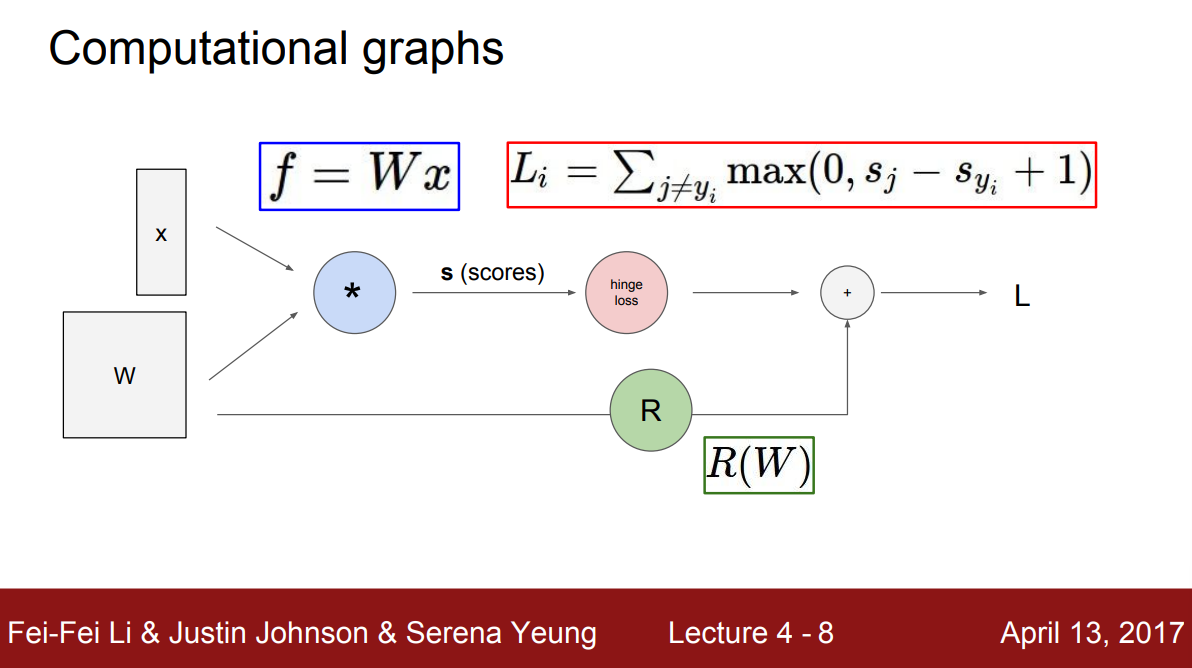
그래프의 각 노드는 연산을 나타내는데, 위의 예에서 곱셈 노드는 행렬 곱을 나타낸다. 파라미터 $W$와 데이터 $x$의 행렬 곱을 곱한 결과로 $s$라는 점수 벡터가 된다는 것을 나타낸다. hinge loss는 $\max$연산을 수행하는 노드로 데이터 항 $L_i$를 계산한다. 오른쪽 하단의 $R(W)$ 노드는 식에는 나와있지 않지만 regularization 항을 계산하는 노드이고, 최종 loss $L$은 데이터 항과 regularization항의 합이 된다.

역전파 (Backpropagation)

함수를 계산 그래프로 나타내는 이유는 역전파(backpropagation)를 사용하기 위함이다. 역전파는 계산 그래프 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용해서 gradient를 계산하는 기술이다.

다음과 같은 함수 $f(x,y,z)$이 있을 때, $f$의 출력 값에 대한 각 변수의 gradient를 계산해보자.

항상 먼저 함수 $f$를 계산 그래프로 나타낸다. 그림의 오른쪽을 보면 $x$, $y$에 대한 덧셈 노드가 있고 그 다음 연산을 위한 곱셈 노드도 볼 수 있다. 그런 다음 그래프에 입력 값인 $x=-2$, $y=5$, $z=-4$를 전달한다. 그래프를 통과하면서 $f$의 출력 값을 계산하는데, 각 노드의 옆에 중간 계산 값을 적어놓았다. 그리고 이러한 중간 노드들을 변수로 다뤄보자. $x + y$ 덧셈 노드를 $q$라고 부르고, $q \cdot z$ 곱셈 노드 $f$라고 부를 것이다.

이때 $x$, $y$에 대한 $q$의 gradient $\dfrac{\partial q}{\partial x}, \dfrac{\partial q}{\partial y}$는 각각 $1$, $1$이다. 단순한 덧셈에 대해 편미분한 결과다.

그리고 $q$, $z$에 대한 $f$의 gradient $\dfrac{\partial f}{\partial q}, \dfrac{\partial f}{\partial z}$는 곱셈 규칙에 의해 $z$, $q$가 된다.

이제 결과적으로 우리가 원하는 것인 각 입력 $x$, $y$, $z$에 대한 $f$의 gradient $\dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z}$를 구해보자.

역전파는 Chain rule의 재귀적인 응용이다. 이를 위해 계산 그래프의 가장 마지막에서부터 gradient를 계산한다. 맨 마지막 출력 $f$에 대한 $f$의 gradient $\dfrac{\partial f}{\partial f}$는 당연히 $1$이다.

그 뒤에 있는 $z$에 대한 gradient를 계산해보자. $z$에 대한 $f$의 미분 $\dfrac{\partial f}{\partial z}$은 $q$이기 때문에 gradient는 $3$이다.

다음으로 $q$에 대한 $f$의 gradient를 알아보자. $q$에 대한 $f$의 미분 $\dfrac{\partial f}{\partial q}$는 $z$이므로 graident는 $-4$이다.

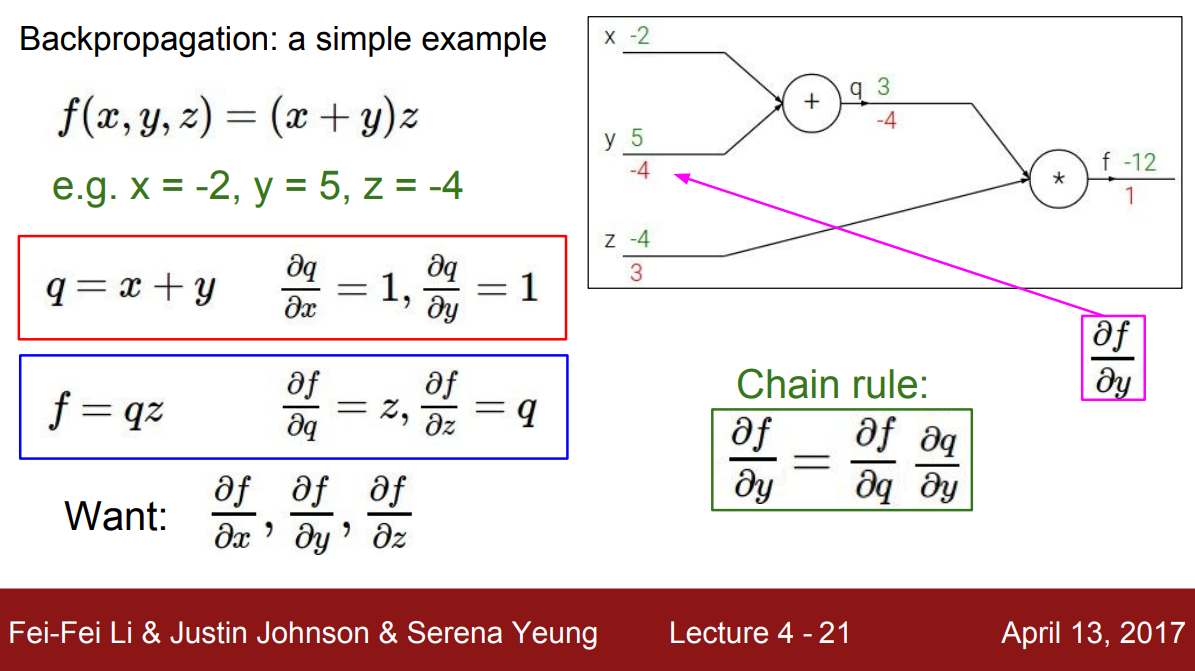
이제 그 뒤으로 가서 $y$에 대한 $f$의 gradient 계산해보자. 그런데 여기서 $y$는 $f$와 그래프 상에서 바로 연결되어 있지 않다. 이때 다음과 같이 chain rule을 이용하여 계산할 수 있다.

\[\dfrac{\partial f}{\partial y} = \dfrac{\partial f}{\partial q} \dfrac{\partial q}{\partial y}\]

즉, $y$에 대한 $f$의 미분 $\dfrac{\partial f}{\partial y}$는 $q$에 대한 $f$의 미분 $\dfrac{\partial f}{\partial q}$과 $y$에 대한 $q$의 미분 $\dfrac{\partial q}{\partial y}$의 곱으로 나타낼 수 있다. 각 항은 $z(=-4)$, $1$과 같으므로 gradient는 $-4$이다.

직관적으로 $y$가 $f$에 미치는 영향을 구하는 과정으로 이해할 수 있다. 만약 $y$를 조금 변화시키면 $q$는 $y$의 영향력만큼 조금 변하게 된다. 여기서는 $y$를 바꿨을 때 $q$에 $1$만큼 영향을 미친다. 마찬가지로 $q$는 $f$에 $z(=-4)$만큼 영향력을 미치므로 이들을 곱해 $y$는 $f$에 $1 \times -4 = -4$만큼 영향력을 미친다고 계산할 수 있는 것이다.

위와 똑같이 $x$에 대한 gradient를 계산해보자. 다시 chain rule을 적용하면, $f$에 대한 $q$의 영향력이 $-4$이고, $x$에 대한 $q$의 영향력은 $1$임을 알고 있으므로 $f$에 대한 $x$의 gradient는 $1 \times -4 = -4$이다.

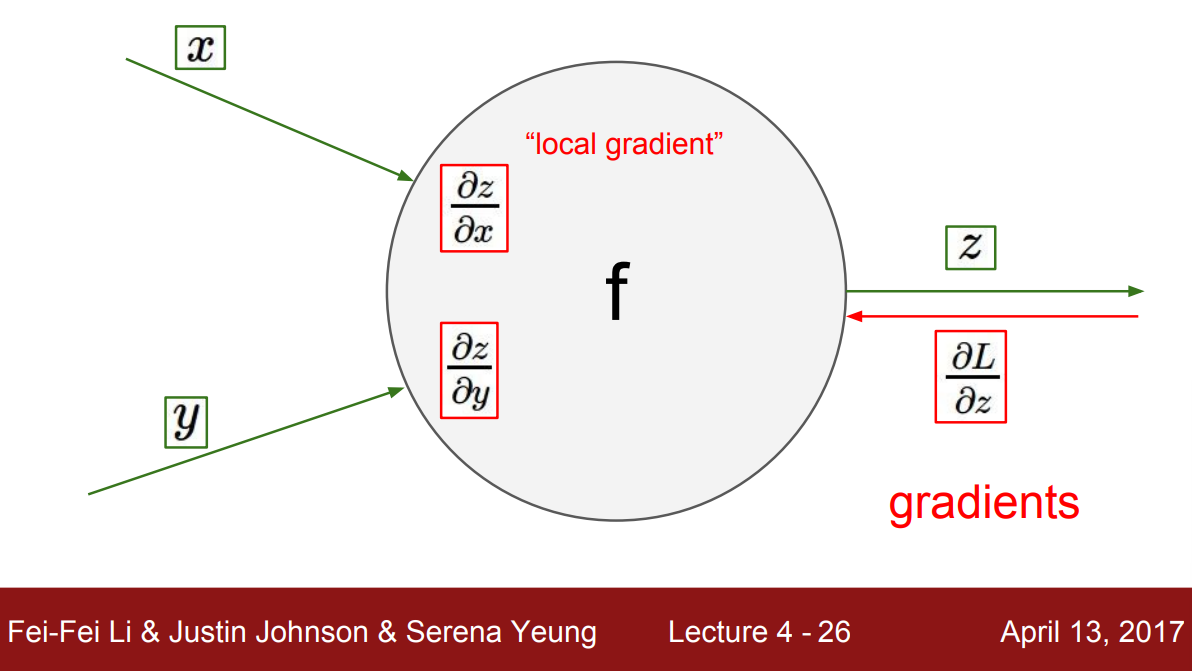
앞에서 설명한 역전파는 계산 그래프 안의 모든 노드에 대해 진행됐다. 그런데 여기서 주목할 점은 각 노드의 계산에는 오직 주변 노드의 정보만 있으면 충분했다.

위 그림은 어떤 노드와 노드의 local 입력 $x$, $y$를 나타낸 것이다. 입력은 노드에 흘러들어와 출력 $z$을 얻게 된다. 그리고 출력에 대한 입력의 변화량인 local gradient를 계산할 수 있다. 여기서 local gradient는 $x$에 대한 $z$의 gradient $\dfrac{\partial z}{\partial x}$와 $y$에 대한 $z$의 gradient $\dfrac{\partial z}{\partial y}$이다. 이때 각 노드 연산은 덧셈 또는 곱셈과 같은 간단한 형태이기 때문에 복잡한 미적분학 없이 아주 쉽게 local gradient를 계산할 수 있다.

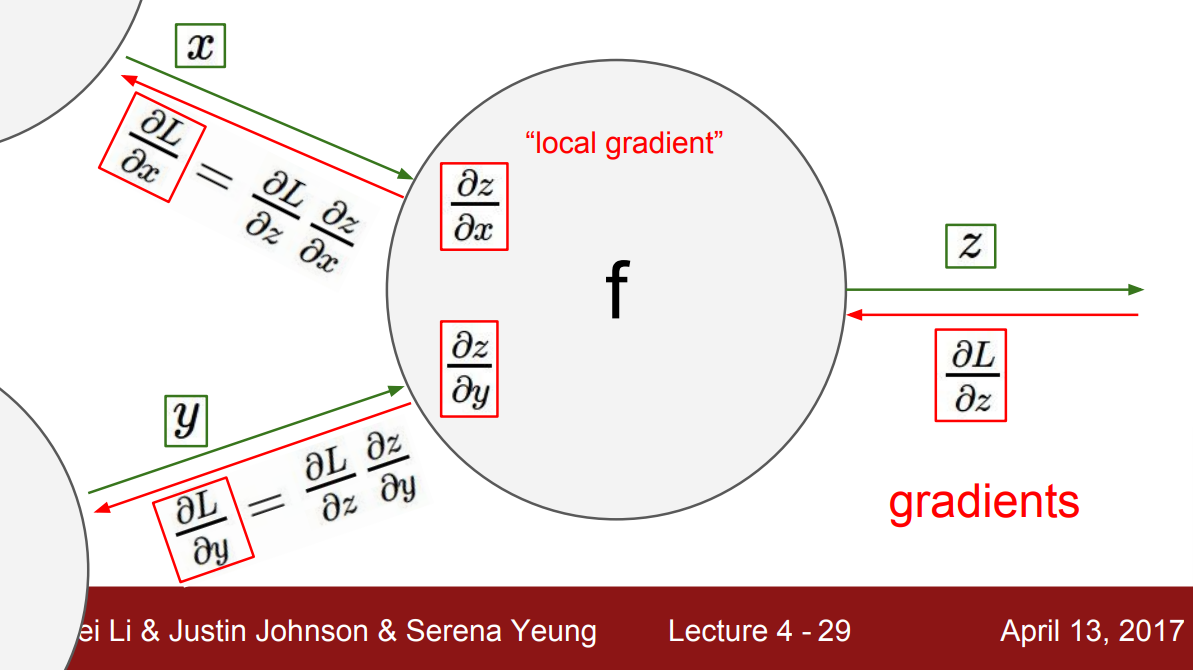
역전파가 전체적으로 어떻게 동작하는지 정리해보자. 그래프의 가장 뒤에서 시작해서 가장 앞 부분으로 gradient가 전파된다. 각 노드에서는 출력 노드의 gradient로부터 local gradient를 계산해서 상류의(입력 쪽의) 노드로 다시 전파한다.

그래서 각 노드에서 $z$에 대한 최종 Loss $L$에 대한 gradient $\dfrac{\partial L}{\partial z}$는 이미 계산되어 있었다. 이 값으로 $x$, $y$에 대한 바로 직전 노드의 gradient를 계산했었고 그 과정에서 chain rule을 사용했었다. $x$에 대한 gradient는 $z$에 대한 gradient와 $x$에 대한 $z$의 local gradient로 합성된다. 이렇게 구한 입력 $x$에 대한 gradient는 그 앞의 노드로 전파됐다. 그래서 chain rule에서는 항상 위쪽으로 gradient가 전파되는 것이다.

중요한 점은 각 노드는 계산하는 과정에서 구한 local gradient 값을 가지고, Backpropagation 시 상위 노드 방향으로 전파되는 gradient를 받아 이 local gradient와 곱하기만 하면 해당 노드의 gradient를 구할 수 있다는 것이다.

예제 (Example)

강의에서 꽤 복잡한 함수에 대한 역전파 과정을 세세하게 되집어주고 있다. 역전파 과정을 충분히 이해했다면 쉽게 받아들일 수 있을 것이다. 링크

결국은 노드마다 간단한 형태의 수식을 정하고 그 유도식을 통해 local gradient를 계산해놓고, 뒤에서 전파되는 gradient와 곱해 다시 전파하는 과정의 반복이다. 여기서 간단한 수식이란 다음과 같은 형태의 함수들을 예로 들고 있다.

\[\begin{align} f(x) &= e^x & \rightarrow & \ & \dfrac{\partial f}{\partial x} &= e^x \\ f(x) &= ax & \rightarrow & \ & \dfrac{\partial f}{\partial x} &= a \\ f(x) &= \dfrac{1}{x} & \rightarrow & \ & \dfrac{\partial f}{\partial x} &= - \dfrac{1}{x^2} \\ f(x) &= c+x & \rightarrow & \ & \dfrac{\partial f}{\partial x} &= 1 \end{align}\]

한 가지 주목할 점은 계산 그래프를 만들 때, 각 노드에 대한 정의를 원하는 대로 세분화 할 수 있다는 점이다. 앞선 예제들에서는 더 이상 쪼갤 수 없는 덧셈, 곱셈으로 노드를 나눴다. 반면, 노드를 더 복잡한 그룹으로 묶을 수 있다는 것이다. 오직 그 노드에 대한 local gradient만 적어 놓으면 역전파 과정은 동일하기 때문이다.

Sigmoid 함수 $\sigma (x)$를 예로 들어보자.

\[\begin{align} \sigma (x) &= \dfrac{1}{1 + e ^ {-x}} \\ \dfrac{d\sigma(x)}{dx} &= \dfrac{e^{-x}}{(1+e^{-x})^2} = (\dfrac{1+e^{-x}-1}{1+e^{-x}})(\dfrac{1}{1+e^{-x}}) = (1-\sigma(x))(\sigma(x)) \end{align}\]

이 함수는 4개의 노드($+$, $\times$, $\exp$, $1/x$)로 나타낼 수도 있겠지만, 이를 직접 미분했을 때 나오는 식인 $(1-\sigma(x))(\sigma(x))$를 계산해냈다면 함수 자체를 큰 노드로 만들 수 있다. 즉, local gradient를 명시할 수 있다면 더 복잡한 노드도 만들 수 있다.

각 노드에서 단순하게 gradient를 계산할지, 많은 수학을 동원하여 간결하고 단순한 그래프를 만들지 사이에서 trade-off를 가진다. 그리고 그 결과로 원하는 만큼 복잡한 형태의 계산 그래프를 활용할 수 있는 것이다.

Patterns in backward flow

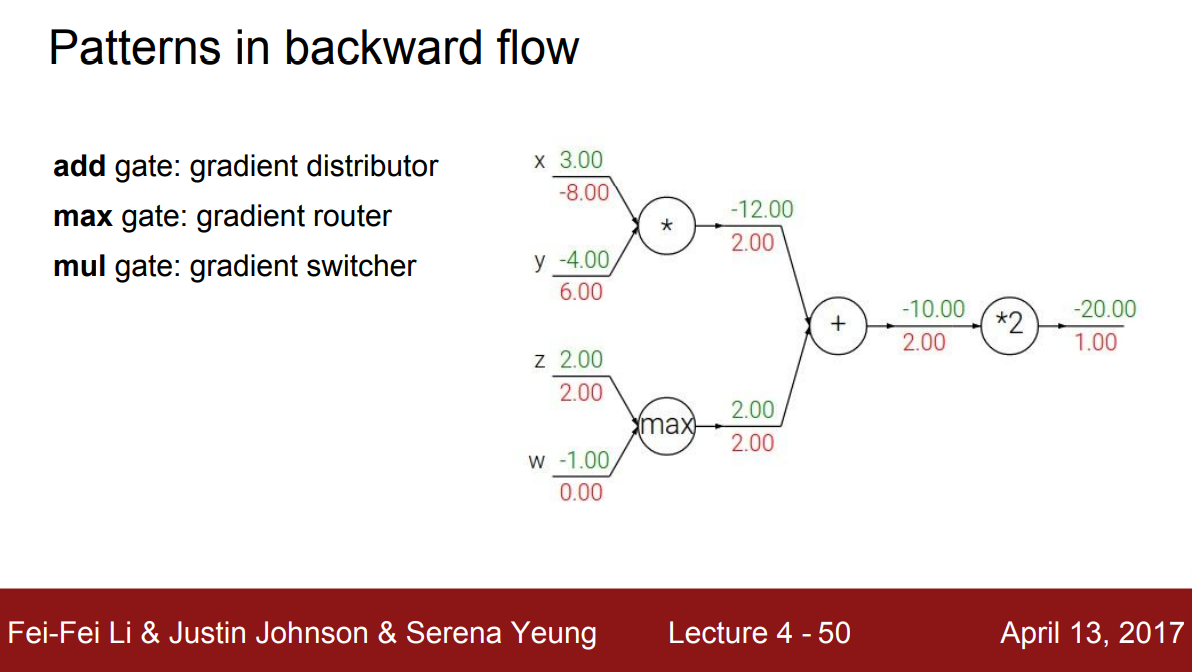
역전파 과정을 직관적으로 해석할 수 있는 패턴이 있다. 덧셈의 경우를 보면 위에서 흘러온 gradient를 연결된 두 입력 노드에 정확히 같은 값으로 나눠준다. 즉, gradient distributor로 볼 수 있다. Max 노드는 흘러온 gradient를 두 입력 노드 중 더 큰 입력 값을 넘긴 노드에게만 전달한다. 다른 노드는 0의 gradient가 흐른다. 즉, gradient router라고 생각할 수 있다. Forward 과정에서 두 노드 중 큰 입력 값을 가진 노드만 함수 계산에 영향을 줬기 때문에 다시 gradient가 전달되어 올 때 그 노드만 고려되는게 자연스럽다. 곱셈 노드는 gradient를 받아 다른 입력노드의 값들로 scaling해서 전달한다. 그래서 gradient switcher로 볼 수 있는 셈이다.

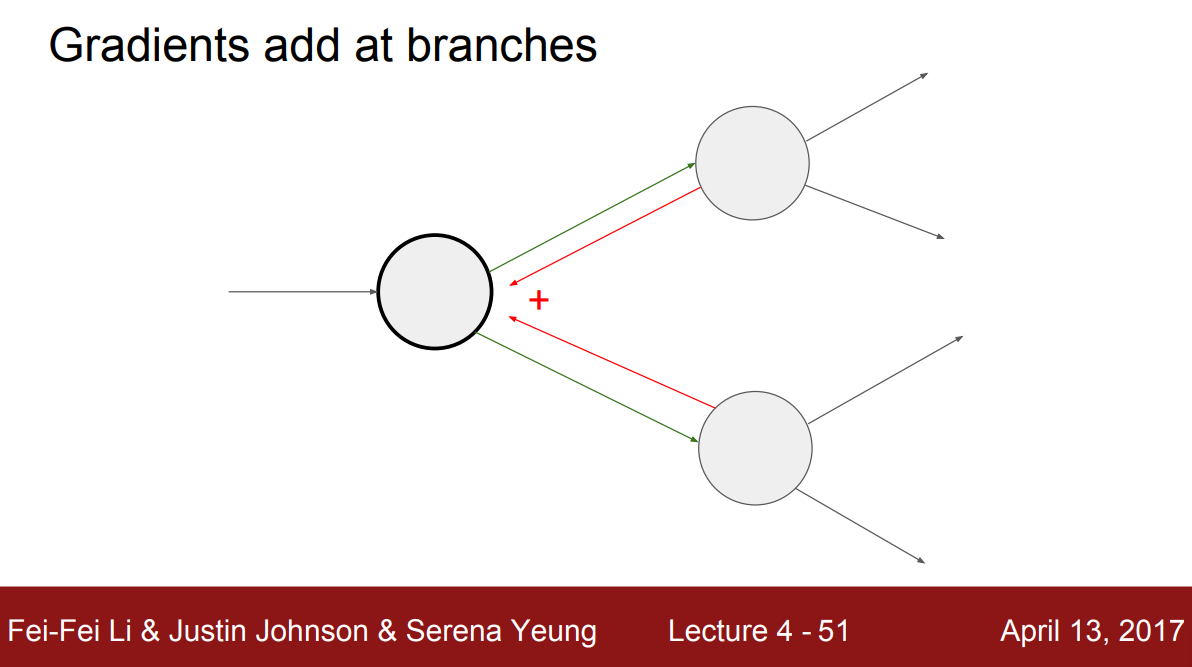
어떤 노드가 여러 노드와 연결되어 있는 경우, 이 노드의 gradient는 위에서 흘러온 gradient들을 합산한 것과 같다. 직관적으로 이 노드가 조금 변할 때, forward pass시 그래프를 따라 연결된 모든 노드들에게 영향을 미친다. 그리고 역전파 시 두 개의 gradient들이 흘러와 다시 이 노드에 영향을 미친다. 따라서 흘러온 gradient들을 모두 더해야 위에서 흘러온 총 gradient가 되는 것이다.

$x$가 함수 $f$에 대해 다변수(mutli-variate) chain rule로 나타내보자.

\[\dfrac{\partial f}{\partial x} = \sum_{i} \dfrac{\partial f}{\partial q_i} \dfrac{\partial q_i}{\partial x}\]

$x$는 변수 $i$에 의해 여러 요소들 $q_i$와 연결되어 있다. 그리고 chain rule에 따라 최종 출력 $f$에 $q_i$와 같은 중간 요소들이 미치는 영향을 계산하고, 이 노드에서 $x$가 각 중간 요소 $q_i$들이 미치는 영향인 local gradient를 계산한 뒤 이들을 합쳐 gradient를 구하는 과정으로 이해할 수 있다.

Gradient for vectorized code

위에서 다룬 예제들은 모두 계산 그래프의 변수들이 스칼라 값을 가지는 경우였다. 이제 벡터 형태일 때 어떻게 되는지 생각해보자.

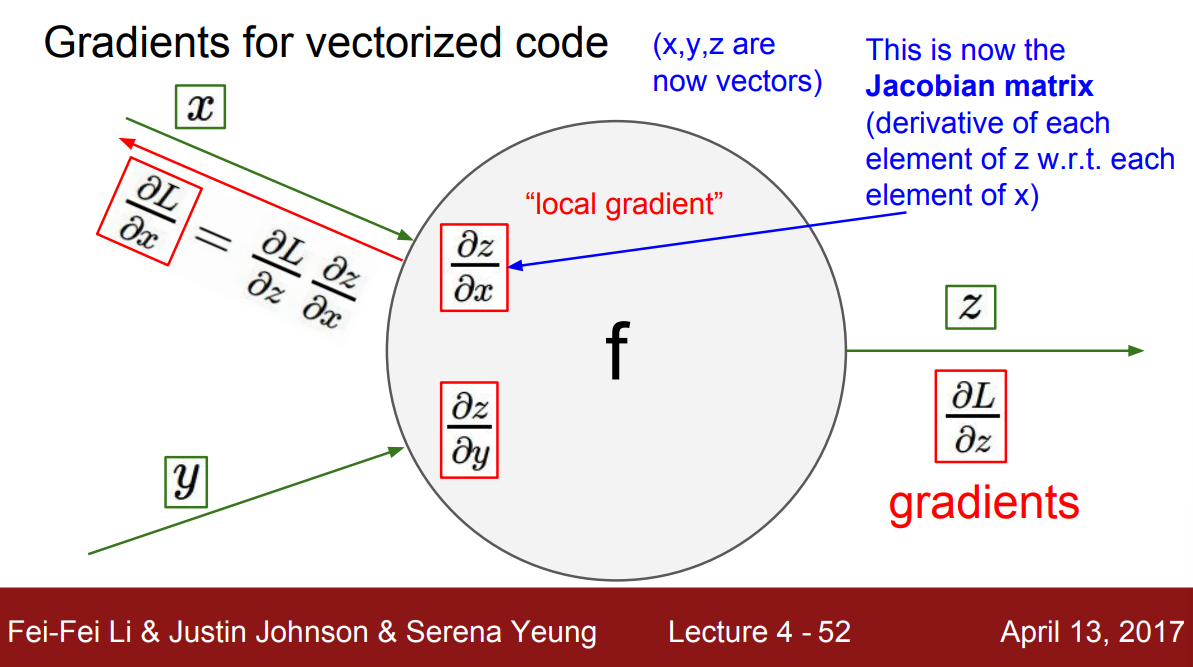
변수 $x$, $y$, $z$는 이제 숫자가 아닌 벡터다. 이에 따라 gradient는 Jacobian Matrix가 될 것이다. 이는 각 요소들의 미분 값을 가지는 행렬이다. 예를 들어, 행렬 $\dfrac{\partial z}{\partial x}$의 각 원소는 $x$의 각 원소에 대한 $z$의 각 원소에 대한 미분을 포함한다.

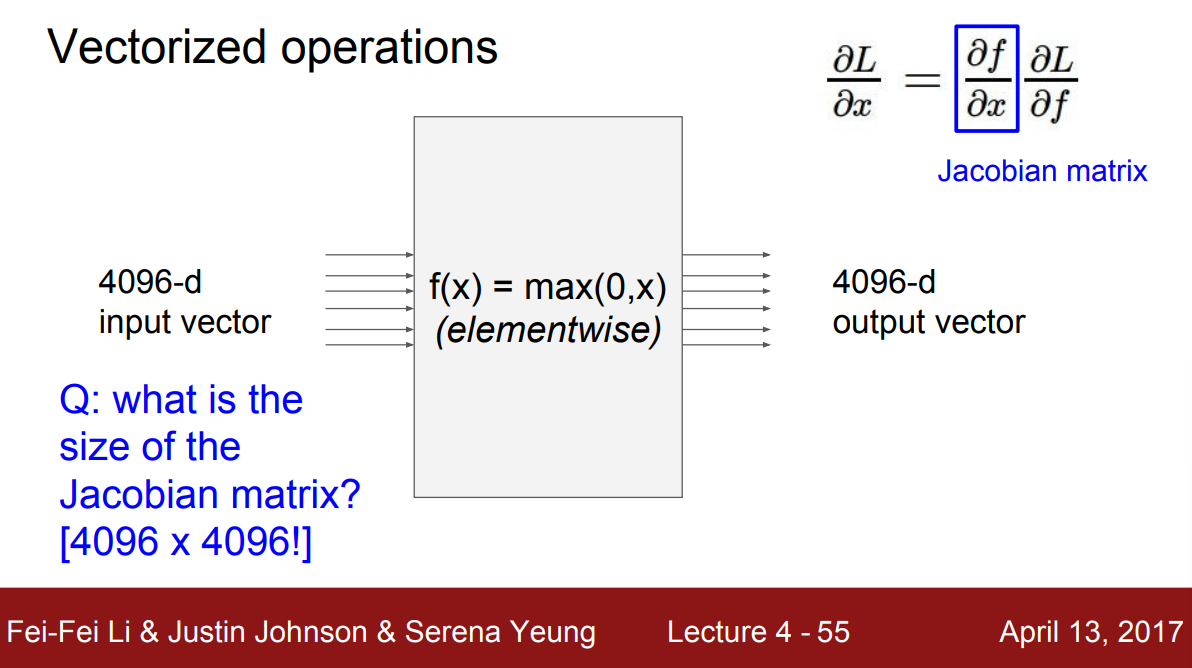
예를 들어 $4,096$차원의 벡터를 요소별로(elementwse) $0$과의 최대값을 취하는 노드를 생각해보자. 출력은 당연히 입력과 같은 $4,096$차원의 벡터이다. 노드의 Jacobian 행렬의 각 행은 입력에 대한 출력의 편미분이다. 즉, $4,096 \times 4,096$ 크기의 행렬이 될 것이다.

만약 입력 $100$개를 묶은 배치로 처리하는 경우 노드는 더 효율적이지만 Jacobian 행렬은 $4,096,000 \times 4,096,000$으로 너무 커지는 문제가 있다. 다행히도 실제로는 이 거대한 행렬을 계산할 필요가 없다. Jacobian 행렬이 어떻게 생겼는지 생각해보면 알 수 있는데 먼저 행렬의 각 원소인 편미분에 대해 생각해보자. 요소별로 $0$과의 $\max$연산을 하는 노드에서 어떤 입력 차원이 어떤 출력 차원에 영향을 줄까? 당연하게도 요소별 연산이므로 각 차원은 같은 차원에 영향을 준다. 이는 행렬에서 대각원소에만 값을 가진다는 뜻과 같고 나머지는 영향이 없기 때문에 Jacobian 행렬은 대각행렬이 된다.

실제로도 전체 Jacobian 행렬을 작성하고 공식화할 필요는 없다. 출력에 대한 $x$의 영향과 이 값을 사용하는 부분에 대해서만 알면 gradient를 계산할 수 있는 것이다.

예제 (A vectorized example)

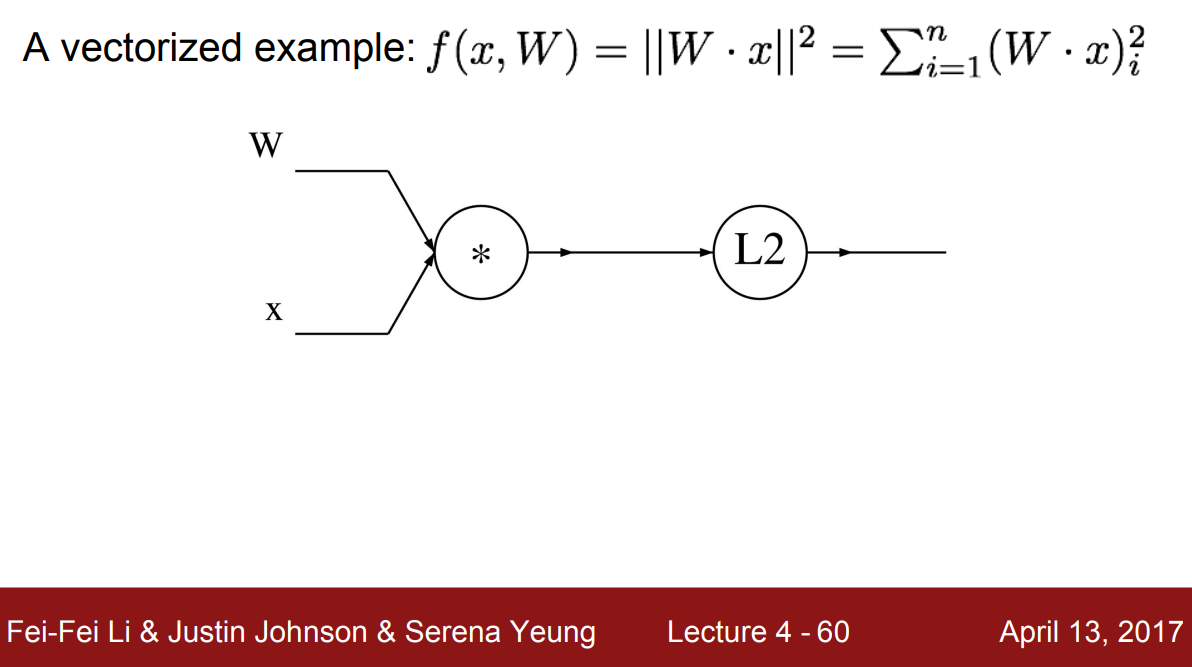
$n$차원의 $x$와 $n \times n$차원의 $W$에 대한 함수 $f(x,W) = \lVert W \cdot x \rVert ^2$를 에로 들어보자. 계산 그래프는 위에서 볼 수 있듯이 $W$와 $x$를 곱셈 노드로 이은 뒤, $\mathrm{L2}$ 노드가 뒤따른다.

$n=2$를 예로 들면, $x$는 $2$차원 벡터가 되고 $W$는 $2 \times 2$ 크기의 행렬이 된다. 그리고 중간 노드인 $W$와 $x$의 곱셈 결과를 $q$라고 하자. $q$는 $W$와 $x$의 요소별 곱셈의 합으로 나타낼 수 있다. 그리고 $f$를 $q$에 대해 정리한 $f(q)$는 $q$의 L2 norm이고 이는 $q_1^2$부터 $q_n^2$까지 합친 것과 같다.

이제 역전파를 해보자. $f$에 대한 $f$의 gradient는 당연히 $1$로 시작한다. 그런 다음 L2 노드 뒤로 gradient를 전파하기 위해서는 L2 노드 이전 중간 변수인 $q$에 대한 gradient를 구해야 한다. 이때 $q$는 2차원 벡터이므로 $q$에 대한 gradient 역시 2차원 벡터의 형태를 가진다. $q$ 각각의 요소가 $f$의 최종 출력에 영향을 얼마나 미쳤는지를 벡터로 구한 것이기 때문이다.

$q$의 각 요소 $q_i$에 대한 $f$의 미분은 $2q_i$이고 이들을 각 요소로 가지는 gradient는 $\nabla _q f = 2q$로 나타낼 수 있다. 즉, L2 노드에서의 gradient 계산은 $q$를 가져와서 $2$를 곱해 뒤로 전파하는 것과 같다.

한 번 더 뒤에 있는 노드로 가보자. $W$에 대한 $q$의 local gradient를 계산하기 위해서 $W$의 각 요소가 $q$의 각 요소에 미치는 영향을 알아보자. 사실 이것은 앞에서 말한 Jacobian 행렬과 같다.

여기서 $q$는 $W \cdot x$이다. 즉, $W_{i,j}$에 대한 $q$의 $k$번째 요소의 gradient는 해당 요소의 $x_j$값과 같다. $(\dfrac{\partial q_k}{\partial W_{i,j}} = \mathbf{1}_{k=i} x_j)$

이때 $\mathbf{1}_{k=i}$는 $k=i$이면 $1$, 아니면 $0$이라는 뜻이다.

그런 다음 각 $W_{i,j}$마다 $f$에 대한 gradient를 찾기 위해 chain rule을 사용해보자. 여기서 $q_k$에 대한 $f$의 미분 $\dfrac{\partial f}{\partial q_k}$을 $W_{i,j}$의 각 요소인 $\dfrac{\partial q_k}{\partial W_{i,j}}$과 합성한다. 그래서 우리는 $W$의 각 요소들이 $q$의 각 요소 대해 미치는 영향을 계산하는 식을 정리했고, $q$의 모든 요소들에 대해 이를 더했다. 결과적으로 식을 정리하면 $2q_ix_j$와 같은 식을 얻을 수 있고, $W$에 대한 gradient를 계산할 수 있다

마지막으로 x에 대한 gradient를 구하자. $x$의 $i$번째 요소 $x_i$에 대한 $q$의 $k$번째 요소 $q_k$에 대한 미분은 $W_{k,i}$임을 알 수 있다. 마찬가지로 chain rule을 적용해 식을 정리하면 $\nabla _x f = 2W^T \cdot q$과 같은 식을 얻을 수 있고 이는 $x$와 같은 모양을 가지는 $x$에 대한 gradient가 된다.

Modularzied implementation

앞서 배운 방식들은 모듈화된 구현이 가능하다. 각 노드를 local하게 보면서 upstream gradient와 함께 chain rule을 이용해 local gradient를 계산했다. 이를 forward pass, backward pass의 API로 생각할 수 있다. forward pass에서는 입력을 받아 노드의 출력을 계산하는 함수를 구현하고, backward pass에서는 chain rule에 따라 gradient를 계산하는 것이다.

이렇게 구현해둔다면 노드(= 게이트)로 이뤄진 전체 그래프를 만들어 모든 노드를 반복해서 호출함으로써 전체 그래프의 forward pass를 계산할 수 있다. 단, 위치적으로 순서를 잘 정렬해서 어떤 노드를 처리하기 전에 이 노드로 들어오는 모든 입력 노드가 먼저 처리되도록 호출해야할 것이다. backward pass도 마찬가지로 역순서로 모든 게이트를 거꾸로 호출한다.

다음 곱셈 게이트를 보자. x, y를 입력으로 받아 결과로 z를 반환한다. backward로 진행할 때는 upstream gradient인 dz를 입력받아 x와 y에 gradient를 전달한다. (예제에서는 scalar 값을 쓰고 있음)

그리고 forward시 중요한 점은 forward pass시 값을 저장(cache)해야한다는 것이다. forward pass가 끝나고 bacward pass에서 이 값이 필요하기 때문이다. 곱셈 게이트의 경우, gradient에 이전 입력 값을 switch하여 곱해주기 때문에 반드시 forward시 입력 값이 필요하다는 것을 알 수 있다.

실제 유명한 딥러닝 프레임워크들 또한 이러한 모듈화를 따른다. 코드를 볼 수 있는 Caffe의 경우, layer라고 부르는 폴더를 보면 computational mode의 전체 목록을 볼 수 있다. 앞에서 예로 든 sigmoid를 비롯해서 convolution, argmax 등 실제로는 더 복잡한 수준으로 모듈화되어 있는 것을 알 수 있다.

Caffe의 sigmoid layer를 보면 실제로 sigmoid와 똑같은 계산을 수행하고, backward pass에서도 upstream gradient인 top-diff를 취해 계산한 local gradient와 곱해주는 것을 알 수 있다.