Gumgood  
CP Algorithm

Kickstart 2021 Round G 개인 풀이

By Sangwon Lee Posted Oct 19, 2021

학교 K관 랩실에서 대회에 참가했는데 중간에 랩실을 닫는 바람에 끝까지 할 수 없었다. A, B번까지 해결했을 때 등수가 괜찮았고 지하철에서 C번을 해결하면서 D번 풀이까지 세웠으나 대회가 끝나버렸다. 결과는 아쉽지만 풀이가 맞았다는 것과 시간이 있었으면 모두 해결할 수 있었다는 것에 의의를 두려고 한다.

A. Dogs and Cats

개 사료가 D개, 고양이 사료가 C개 있다. 개 또는 고양이로 이뤄진 N마리의 동물들에게 순서대로 각자의 사료를 하나식 먹인다. 그런데 개 사료를 하나 줄 때마다 고양이 사료가 M개식 추가된다(??). 이 때 모든 개들에게 사료를 줄 수 있는지 판단하는 문제다.

시뮬레이션하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include<bits/stdc++.h>
using namespace std;
using lint = long long;

int n;
lint d, c, m;
char s[10001];

bool solve() {
    int i = 0;
    for (i = 0; i < n; ++i) {
        if (s[i] == 'D') {
            if (d--) c += m;
            else break;
        }
        else {
            if (c--);
            else break;
        }
    }
    for (; i < n; ++i)
        if (s[i] == 'D') return false;
    return true;
}

int main() {
    int tc; scanf("%d", &tc);
    for (int tt = 1; tt <= tc; ++tt) {
        scanf("%d%lld%lld%lld%s", &n, &d, &c, &m, s);
        bool ans = solve();
        printf("Case #%d: %s\n", tt, ans ? "YES" : "NO");
    }
}

B. Staying Hydrated

2차원 평면에 K개의 직사각형이 있다. 모든 직사각형까지의 멘헤튼 거리 합이 최소인 좌표를 출력하는 문제다. 직사각형 내부의 점은 거리가 0이다. 만약 정답이 여러 개인 경우 x좌표가 작은 것을, x좌표도 같다면 y좌표가 작은 것을 출력한다.

멘헤튼 거리의 합을 구하는 문제이기 때문에 x좌표와 y좌표를 분리해서 생각할 수 있다. 따라서 일직선 상에 K개의 선분이 있고 모든 선분까지의 거리의 합이 최소인 좌표를 구하는 문제가 되었다.

이는 스위핑 알고리즘으로 해결할 수 있다. 스위핑하면서 현재 지점을 포함하는 선분은 무시하고, 왼쪽과 오른쪽에 있는 선분에 대한 거리를 계산해서 답을 찾아주면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

#include<bits/stdc++.h>
using namespace std;
using lint = long long;
const int INF = 1e9 + 9;

int k, sx[100000], sy[100000], ex[100000], ey[100000];

int solve(int s[], int e[]) {
    map<int, pair<int, int>> io;
    for (int i = 0; i < k; ++i)
        io[s[i]].first++, io[e[i]].second++;

    lint prv = -INF, dist = 0;
    for (int i = 0; i < k; ++i)
        dist += s[i] - (-INF);

    lint l = 0, m = 0, r = k;
    lint mn = dist, ret = -INF;
    for (auto [x, inou] : io) {
        auto [in, ou] = inou;
        dist += l * (x - prv);
        dist -= r * (x - prv);
        l += ou;
        r -= in;
        prv = x;
        if (mn > dist) mn = dist, ret = x;
    }
    return ret;
}

int main() {
    int tc; scanf("%d", &tc);
    for (int tt = 1; tt <= tc; ++tt) {
        scanf("%d", &k);
        for (int i = 0; i < k; ++i)
            scanf("%d%d%d%d", sx + i, sy + i, ex + i, ey + i);
        int x = solve(sx, ex);
        int y = solve(sy, ey);
        printf("Case #%d: %d %d\n", tt, x, y);
    }
}

C. Banana Bunches

길이가 $N$인 수열 $B$에 대해 서로 겹치지 않는 두 개의 연속한 부분 수열을 골라 합이 $K$를 만들려고 한다. 가능하다면 두 수열 길이의 합을 최소로 만드는 문제다.

$B[0..i]$의 모든 연속한 부분 수열에 대해 합과 최소 길이를 저장하자. 그러면 $i+1$에서 시작하는 연속하는 부분 수열의 합 $SUM$에 대해 $K-SUM$에 대한 최소 길이를 바로 알 수 있다. 모든 $SUM$은 부분 수열의 길이를 순차적으로 늘려가면서 구하면 $O(N)$에 수행할 수 있다. 이를 모든 $i$에 대해 처리해주면 $O(N^2)$에 해결할 수 있다.

주의할 점은 연속한 부분 수열의 합이 $K$ 이하인 경우만 저장해서 $O(1)$에 처리해야한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

#include<bits/stdc++.h>
using namespace std;
using lint = long long;
const int INF = 1e9 + 9;

int n, k, b[5000];

int mn[1000001];

int solve() {
    int ret = INF;
    fill(mn, mn + 1000001, INF);

    // 2-seg
    for (int i = 0; i < n; ++i) {
        lint psum = 0;
        for (int j = i; j < n; ++j) {
            psum += b[j];
            if(psum > k) break;
            ret = min(ret, mn[k - psum] + j - i + 1);
        }

        psum = 0;
        for(int j=i;~j;--j){
            psum += b[j];
            if(psum > k) break;
            mn[psum] = min(mn[psum], i - j + 1);
        }
    }

    // 1-seg
    ret = min(ret, mn[k]);

    return ret;
}

int main() {
    int tc; scanf("%d", &tc);
    for (int tt = 1; tt <= tc; ++tt) {
        scanf("%d%d", &n, &k);
        for (int i = 0; i < n; ++i)
            scanf("%d", b + i);

        int ans = solve();
        printf("Case #%d: %d\n", tt, ans == INF ? -1 : ans);
    }
}

D. Simple Polygon

N개의 변을 가지면서 넓이가 A/2인 단순 다각형을 생성하는 문제다.

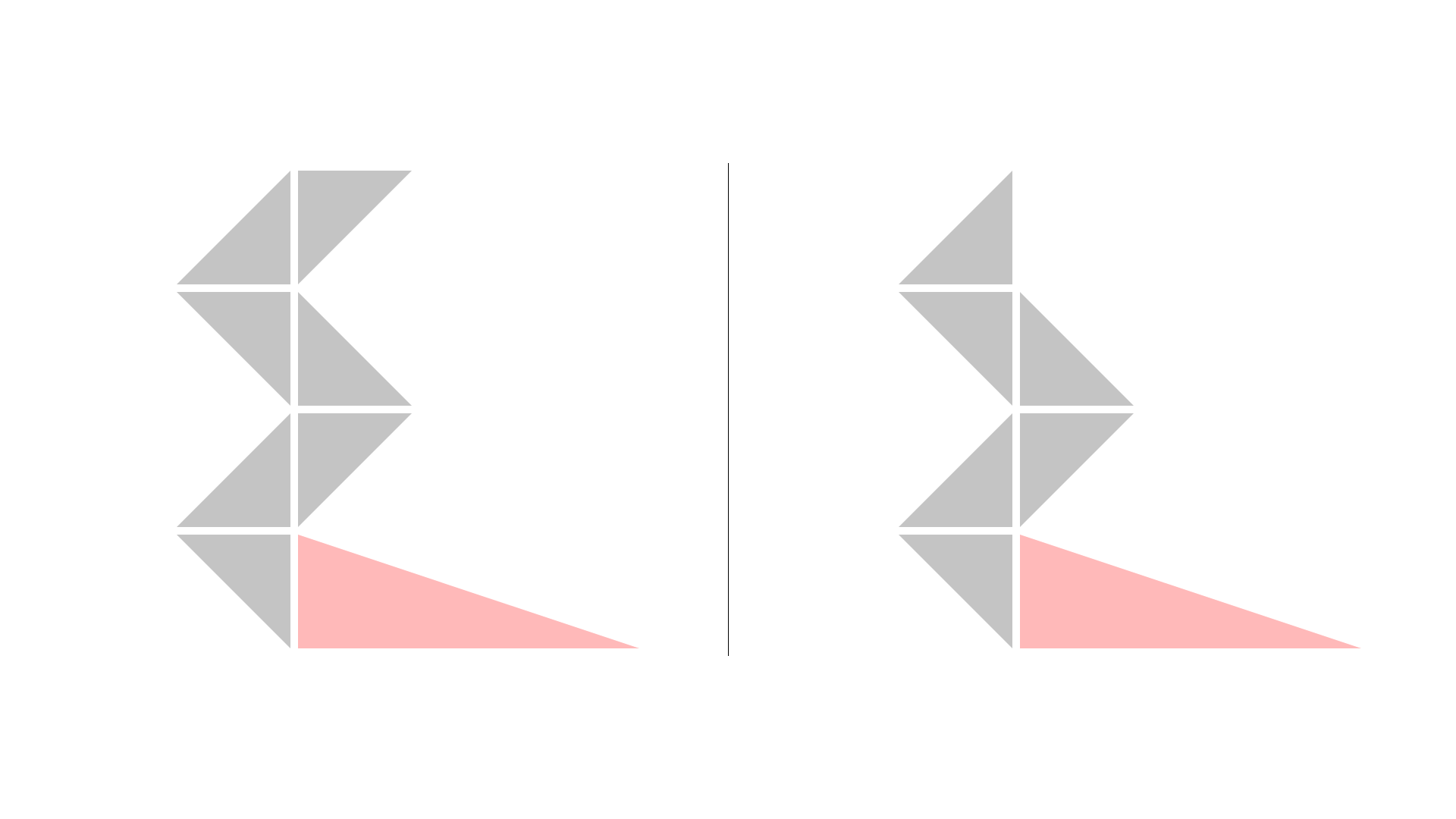
정수 좌표를 가지는 다각형 중 가장 작은 넓이를 가지는 다각형은 넓이가 1/2인 삼각형이다. 이러한 삼각형을 한 변만 맞대도록 이어 붙이면, 최소 넓이로 최대 개수의 변을 가지는 다각형을 만들 수 있다.

먼저 다음과 같은 다각형을 만들자. (왼쪽은 N이 짝수인 경우, 오른쪽은 N이 홀수인 경우이다.)

이는 최소 넓이의 다각형이므로 한 삼각형을 골라 A/2까지 모자란 넓이만큼 늘려주면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#include<bits/stdc++.h>
using namespace std;
using lint = long long;

int n, a;

vector<pair<int, int>> solve() {
    vector<pair<int, int>> ret, rev;
    if (n == 3) {
        ret.emplace_back(0, 0);
        ret.emplace_back(1, 0);
        ret.emplace_back(0, a);
        return ret;
    }

    if (a + 2 < n) return ret;

    ret.emplace_back(2, 0);
    ret.emplace_back(1, 0);
    for (int i = 1; i * 2 < n; ++i) {
        ret.emplace_back(i % 2 ? 0 : 1, i);
        rev.emplace_back(i % 2 ? 1 : 2, i);
        a -= 2;
    }
    if (n % 2) rev.pop_back(), a++;

    reverse(rev.begin(), rev.end());
    for (auto it : rev) ret.emplace_back(it);
    ret.front().first += a;

    return ret;
}

int main() {
    int tc; scanf("%d", &tc);
    for (int tt = 1; tt <= tc; ++tt) {
        scanf("%d%d", &n, &a);

        vector<pair<int, int>> ans = solve();
        printf("Case #%d: ", tt);
        if (ans.empty())
            puts("IMPOSSIBLE");
        else {
            puts("POSSIBLE");
            for (auto [x, y] : ans)
                printf("%d %d\n", x, y);
        }
    }
}
kickstart, google