프로그래머스 월간 코드 챌린지 시즌3 9월

참가후기

전체 6등을 했다. 참 괜찮은 국내 알고리즘 대회 중 하나이지만 플랫폼의 단점이 많다. 테스트 케이스를 추가하는 과정이 번거롭고, 디버깅용 출력을 너무 많이 하면 또 실행이 안된다. 무엇보다도 대회 종료 전에 코드를 따로 백업해두지 않으면 작성한 코드가 모두 날아가는 것이 가장 불편하다.

깜박하고 코드를 백업해두지 않아서 이번에는 코드 없이 풀이만 올린다. ㅜㅜ

A. 없는 숫자 더하기

$0$부터 $9$까지 숫자에 대해 배열을 순회하면서 없으면 답에 누적해주면 된다.

B. 빛의 경로 사이클

각 격자칸을 네 개의 정점으로 나누면 다음과 같이 나타낼 수 있다.

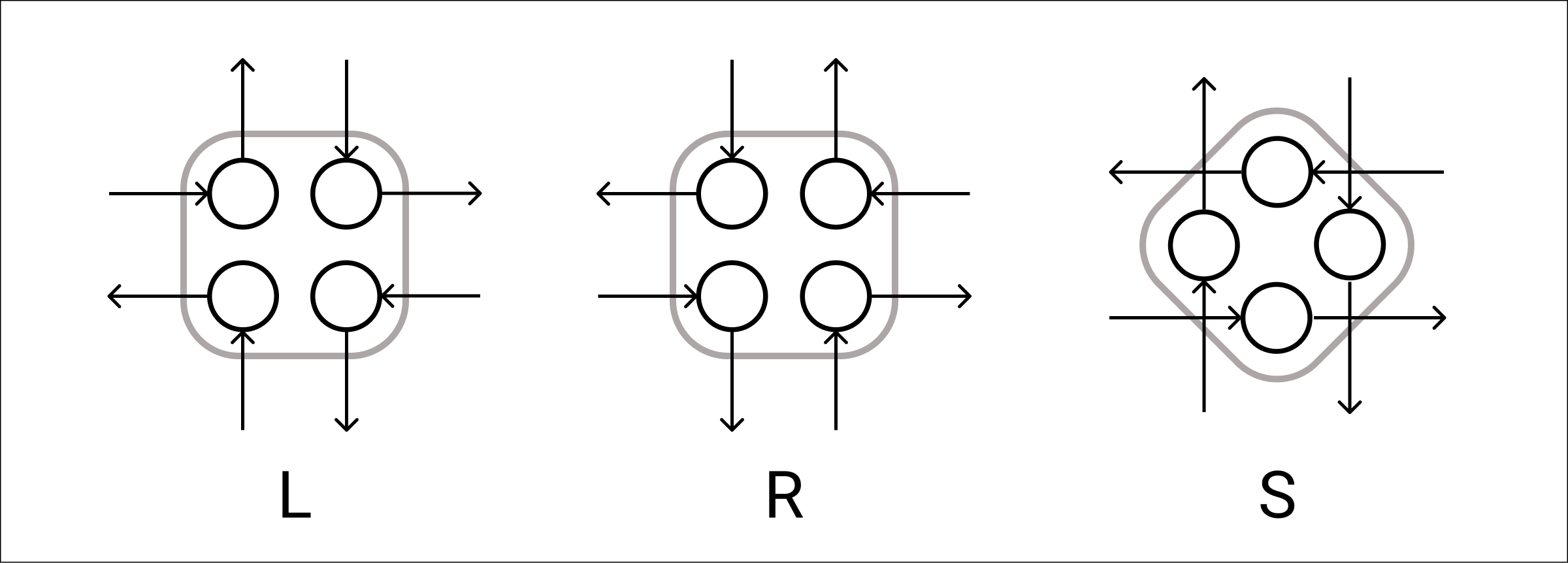
이렇게 만들어진 그래프의 모든 정점의 indegree와 outdegree가 같기 때문에 연결된 모든 정점에 대한 오일러 경로가 존재한다. 게다가 indegree와 outdegree가 정확히 $1$이기 때문에 오일러 경로는 유일하다. 즉, 정확히 하나의 사이클이 만들어 지게 된다. 따라서 연결된 정점들의 집합인 컴포넌트 개수를 세주면 된다.

C. 금과 은 운반하기

$t$ 시간에 금 $a$kg과 은 $b$kg을 전달할 수 있다면 $t+1$ 시간에도 전달가능 하다는 점에 착안하면 binary search로 접근할 수 있다. 그러면 $t$ 시간에 가능한지 결정하는 문제가 된다.

우선 최대한 금을 우선 싣고 남은 공간이 있다면 은을 실었다고 가정하고, 필요한 만큼 금을 은으로 교환하는 식으로 생각해볼 수 있다. 예를 들어, 트럭에 금 8kg와 은 2kg을 실었다고 가정했을 때 금 7kg과 은 3kg으로 바꿔 실으면 금 1kg과 은 1kg을 교환하는 것과 같다는 뜻이다. 금을 우선 실었는데도 부족하면 아예 불가능한 경우이므로 이를 제외하면, 금은 충분하고 은이 부족한 상태일 것이다. 이제 금을 $a$kg빼고 가능한만큼 모두 은으로 교환하여 $b$kg을 채울 수 있는지 확인해주면 된다.

$i$번 도시의 트럭이 도시를 최대 $\lfloor \frac{t + t_i}{2t_i} \rfloor$ 번 방문 가능하기 때문에 최대 $W_i = \min (g_i + s_i, \lfloor \frac{t + t_i}{2t_i} \rfloor \cdot w_i)$ kg의 광물을 운반할 수 있다. 금을 $G_i = min(W_i, g_i)$ 만큼 싣고 은을 $S_i = \min(W_i - min(W_i, g_i), s_i)$ 만큼 실어주면 총 ${E_i} = min(G_i, s_i - S_i)$만큼 교환 가능한 상태가 된다.

모든 $i$에 대해 $G_i$, $S_i$, $E_i$를 계산해두고 $\sum{G_i} \ge a \ \land \ \sum{S_i} + \min(\sum{E_i}, \sum{G_i} - a) \ge b$ 임을 확인해주면 된다. 이를 $O(N)$에 계산하면 전체 $O(N \log T)$에 해결할 수 있다.

D. 안티세포

배열 $C$에 $i$를 $j$번 추가하려면 맨 뒤에 있는 $j$개의 안티세포들은 합이 $b[i] \cdot 2^{j-1}$, $b[i] \cdot 2^{j-2}$, $…$, $b[i] \cdot 2^0$이어야 한다. 뒤에서부터 순서대로 합쳐지면 $i$가 $j$번 추가되면서 합이 $b[i] \cdot 2^{j}$인 안티세포가 될 것이다.

배열 $C$에 $i$를 $j-1$번 추가할 수 있었고 여기에는 $[k,i]$ 구간의 안티 세포가 합쳐졌다는 사실을 안다고 하자. 이 때, $b[k-1] \cdot 2^p = b[i] \cdot 2^{j-1}$인 $p$가 존재하고 배열 $C$에 $k-1$을 $p$번 추가할 수 있다면 배열 $C$에 $i$를 $j$번 추가하는게 가능해진다. 이를 dp식으로 정리하자.

• $dp[i][j] :=$ (배열 $C$에 $i$를 $j$번 추가할 수 있는 경우의 수)

다음과 같이 점화식을 세울 수 있다.

• $dp[i][j] = \sum_{(p,k) \ \in \ {p,k\ \vert \ b[k-1] \cdot 2^p = b[i] \cdot 2^{j-1} } }{dp[k-1][p]}$

$j$는 가장 큰 경우 $\log(2e15)$까지 가능하기 때문에 dp테이블의 크기는 $O(N \log(2e15))$이고 각 $dp[i][j]$에 대해 $p$와 $k$를 binary search로 찾으면 전체 $O(N \log (2e15) \log N)$에 해결할 수 있다.

공식 해설에서 소개하는 정해는 $O(n \log \max b)$라고 한다.