-
CS231n Lecture 1: Introduction
Stanford의 CS231n은 컴퓨터 비전(computer vision) 분야에서에서 가장 인기있는 강의 중 하나다. 그 중에서도 신경망(neural network), 특히 CNN과 관련된 부분에 초점을 맞추고 있다. 감사하게도 강의 녹화본이 공개되어 있다. 이번에 강의를 들어보면서 컴퓨터 비전으로서의 딥러닝에 대한 깊은 이해를 해보려고 한다. 순...
-
Ubuntu 서버에 Docker로 Tensorflow 개발 환경 구축하기
Ubuntu 서버에 Tensorflow 개발 환경을 구축할 일이 생겼다. 다양한 환경의 여러 오픈 소스들을 돌려보기도 해야하고, 혼자 쓰는 서버가 아니기 때문에 Docker를 활용하기로 했다. 하지만 세팅하는 과정이 생각보다 어려워서 이렇게 따로 정리해두려고 한다. 1. 서버 GPU 확인 서버에는 NVIDIA GPU가 장착되어 있고 이를 지원하기 ...
-

Kickstart 2021 Round G 개인 풀이
학교 K관 랩실에서 대회에 참가했는데 중간에 랩실을 닫는 바람에 끝까지 할 수 없었다. A, B번까지 해결했을 때 등수가 괜찮았고 지하철에서 C번을 해결하면서 D번 풀이까지 세웠으나 대회가 끝나버렸다. 결과는 아쉽지만 풀이가 맞았다는 것과 시간이 있었으면 모두 해결할 수 있었다는 것에 의의를 두려고 한다. A. Dogs and Cats 개 사료가 ...
-
프로그래머스 월간 코드 챌린지 시즌3 9월
참가후기 전체 6등을 했다. 참 괜찮은 국내 알고리즘 대회 중 하나이지만 플랫폼의 단점이 많다. 테스트 케이스를 추가하는 과정이 번거롭고, 디버깅용 출력을 너무 많이 하면 또 실행이 안된다. 무엇보다도 대회 종료 전에 코드를 따로 백업해두지 않으면 작성한 코드가 모두 날아가는 것이 가장 불편하다. 깜박하고 코드를 백업해두지 않아서 이번에는 코드...
-
접미사 배열과 LCP 배열(Suffix Array and LCP Array)
접미사(Suffix) 문자열 $s$의 $i$번째 접미사란, $s$의 $i$번째 글자부터 마지막 글자까지 포함하는 부분문자열을 뜻합니다. 예를 들어, $s=\mathsf{GATAGACA}$의 접미사를 순서대로 나타내면 다음과 같습니다. [\begin{array}{ c c } ...
-
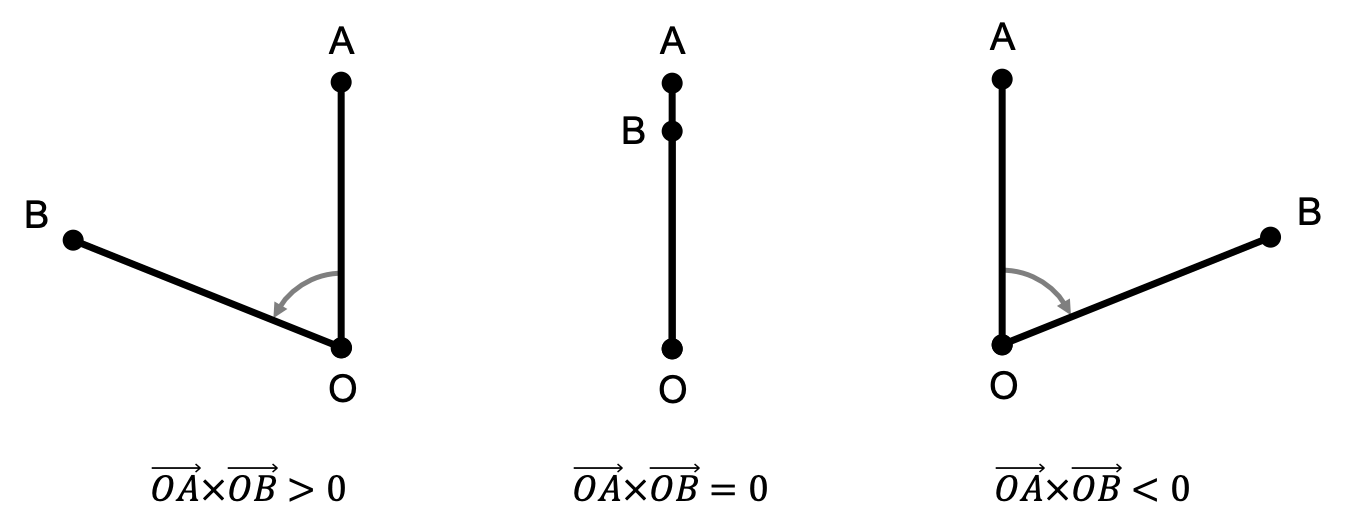
각도 정렬 알고리즘(Sort by Angular)
2차원 좌표평면 상의 점들을 기준점에 대해 반시계 방향 순서로 정렬하는 방법에 대해 알아보겠습니다. 외적을 이용한 방향성 판별 세 점 $O$, $A$, $B$의 방향성은 외적을 통해 판단할 수 있습니다. 외적 $\overrightarrow{OA} \times \overrightarrow{OB}$의 외적이 0보다 크면 반시계 방향(Counter Cl...
-

프로그래머스 월간 코드 챌린지 시즌2 4월
참가후기 전체 8등을 했다. 지문이 간단하고 명확했고 무려 한국어였다(…). 항상 영어 지문을 잘못 해석해서 고생했던 나한테 유리했다. 국내에도 이렇게 좋은 대회가 생기다니 앞으로도 자주 참가해야겠다. A. 음양 더하기 몇 개의 정수들이 있다. 이 정수의 절대값을 나타내는 수열과 부호를 나타내는 boolean 배열이 주어진다. 이 때, 모든 ...
-
Kickstart 2021 Round A 개인 풀이
A. K-Goodness String 문자열 절반을 기준으로 서로 대칭이 아닌 쌍의 개수를 정확히 $K$개로 만들기 위해 최소 몇 개의 문자를 바꿔야하는지 출력하는 문제다. 현재 문자열에서 대칭이 아닌 쌍의 개수를 구하고, $K$와 얼마나 차이나는지 출력했다. 배열 크기를 잘못잡아서 한 번 틀렸다. 1 2 3 4 5 6 7 8 9 10 11 1...
-
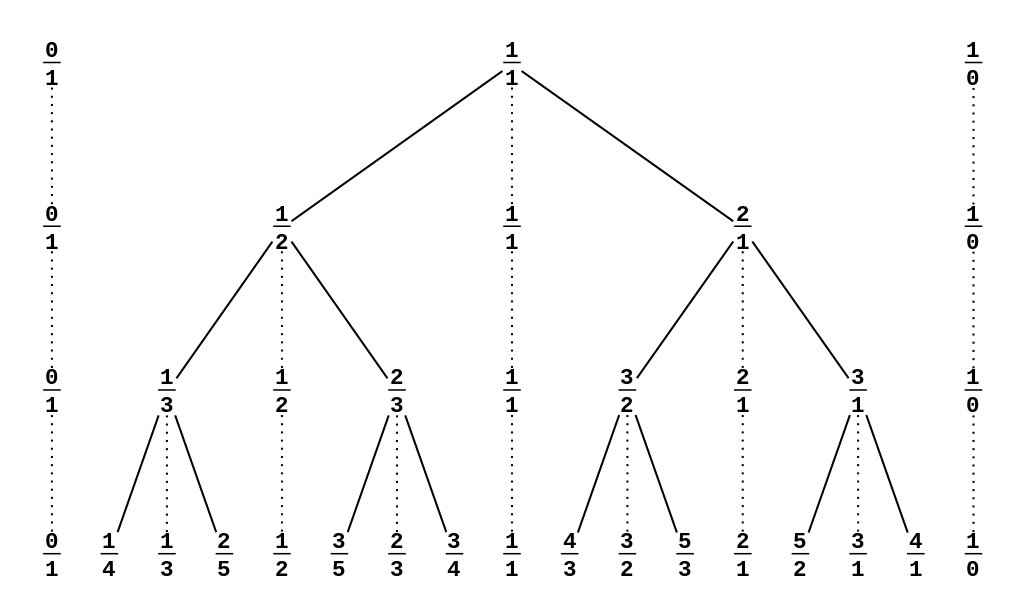
스턴 브로콧 트리(Stern Brocot tree)
먼저, 모든 양의 분수를 나열하는 방법에 대해 알아봅시다. 다음 두 분수가 있습니다. [\dfrac{0}{1}, \dfrac{1}{0}] 두 번째는 엄밀히 분수는 아니지만, 무한대를 나타내는 기약분수로 해석합시다. 매 반복마다, 모든 인접한 분수 $\dfrac{a}{b}$ 와 $\dfrac{c}{d}$ 사이에 mediant인 $\dfrac{a+c...
-
IOI 2011 풀이 (International Olympiad in Informatics 2011)
작성일 기준 BOJ에서 채점 가능한 문제만 풀어보았습니다. 1번. BOJ 5819 열대 식물원 제 풀이는 $O(N + M \log M + Q)$이지만 공식 풀이는 $O(QN)$입니다. 각 연못을 node로 하고 각 산책로에 대해 아름다운 정도를 가중치로 갖는 edge로 directed graph를 구성합니다. 철수가 한 연못에서 다음 연못으...